Amdahl’s Law
We have learnt that running processes in parallel can add to increased capacity and capability, but there is a limit to how can be gained from parallelism.
Travelling to New York
If we want to travel to New York, we need to do two things:
- Check-in at the airport
- Fly to New York

A flight to New York from London is approximately 7hrs 55minutes. But I am required to be at the airport 3hrs before the scheduled departure.
This is a total time therefore of: 10hrs 55minutes.
A Concorde flight to New York from London was approximately 3hrs 30minutes. This was a shorter journey time of over 4hrs.
However, I would still be required to be at the airport 3hrs before the scheduled departure (assuming Concorde flights were still an option).
This is a total time therefore of: 6hrs 30minutes.
As we can see, that although the journey time was less than half, we still on made a time saving of 4hrs 25mins.
What does flying to New York have to do with parallel computing?
Computer programs like our journey to New York have elements that can be optimised via parallelism.
If we had a program with both serial and parallel components, on a single processor the serial component would account for 20% of the runtime of the program.
1 processor:

If we increased the number of processors to 2:
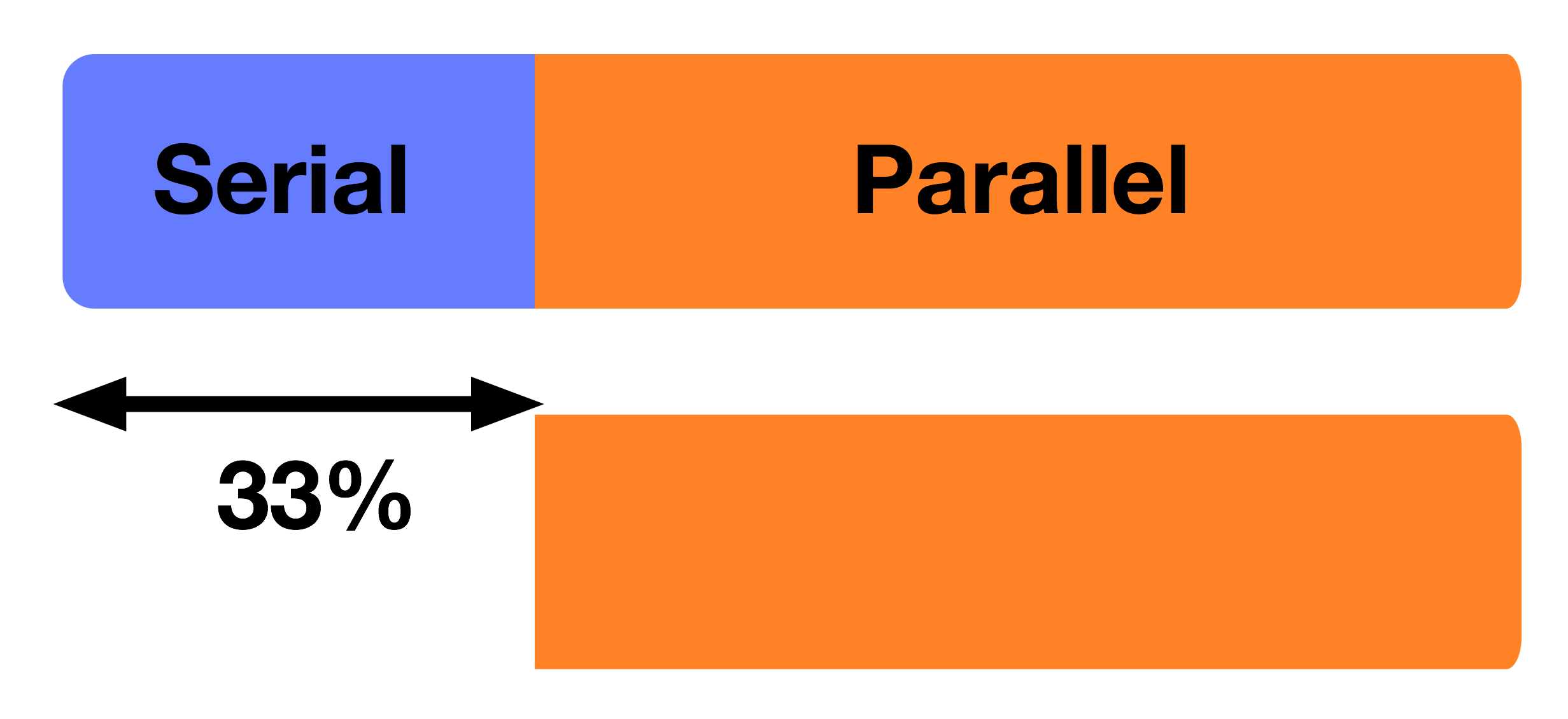
We have reduced the runtime of the parallel component as this is split across the two processors, but have the same runtime for the serial component. This now accounts for 33% of the total runtime.
And if we increased the number of processors to 10:

Amdahl’s Law
The limitations illustrated above are due to Amdahl’s law:
Theoretical maximum speed-up =
Where:
- N is the speedup of the part of the task that benefits from improved system resources, and
- P is the proportion of execution time that the part benefiting from improved resources originally occupied.
The impact of Amdahl’s Law:
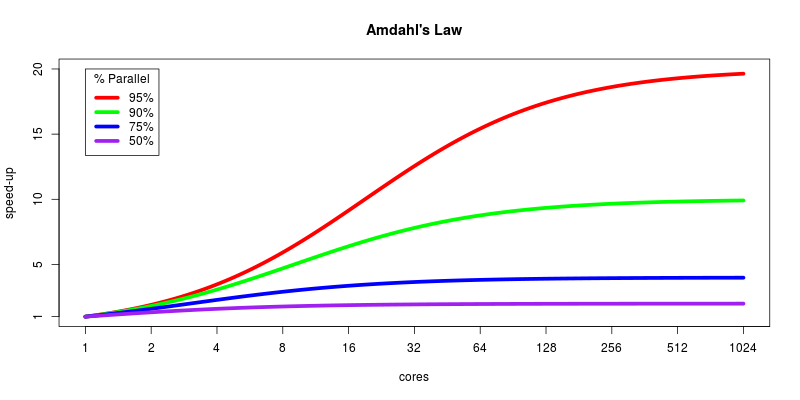
If 95% of the program can be parallelized, the theoretical maximum speedup using parallel computing would be 20x, no matter how many processors are used.